FIRE を実現するには毎月いくら積み立てる必要があるか把握していますでしょうか?
今回は、Excelを活用した シミュレーション 方法をご紹介したいと思います。
実はExcelの関数を用いて必要な入金額は算出することができます。
投資は複利があるから計算が難しいんですよね
今回ご紹介するのはFV関数とPMT関数です。
では、まずは一般論のご紹介です。
FIREに必要な資産額は?
有名なのは「4%ルール」です。
金融資産を利回り4%と仮定した際には、年間支出の25倍の資産があれば理論的に資産は減らないという考え方です。
たとえば、年間支出200万円の場合は、以下のような試算となります。
- 年間支出200万円 × 25倍 = 5000万円(必要資産)
- 資産5000万円 × 利回り4% = 200万円(年間評価益)
- したがって、資産5000万円あれば資産は減らない(年間評価益 =年間支出となる)
つまり上の例でいえば、年間200万円ずつ資産が増える一方、支出も年間200万円なので、翌年も資産5000万円のまま一向に減らない計算になるのです。
もちろんこれは目安なので、不安な方は年間支出を高く見積もったり、利回りを4%未満で試算したりしながら、必要資産の見積もりを微調整します。
これでおおよその目標額は一旦見えてきました。
さて、次に考えるべきはいつまでにそのポジションを築くか?という論点です。
Excelで計算していきます!
目標額から「毎月の積立額」を計算する
たとえば「30年で資産1億円を達成するために、毎月いくら積立が必要か?」を計算で求めるのは簡単ではありません。
計算を複雑にする要因としては、①毎月積み立てていくこと(資産の元手が増える)、②複利が働くこと(評価益が増えていく)、が挙げられます。
それらを考慮したうえで、「必要な毎月の積立額」を算出してくれるのがExcelのPMT関数です。
PMTは「ペイメント」の略です
PMT関数は元々ローンの定期支払額を求めるための関数ですが、
資産運用にもこれを使うことができます。
=PMT(利率, 期間, 現在価値, 将来価値, 支払期日)
以下のExcelをそのまま作っていただき、数値部分(A3、B3、C3セル)のみを変えていただければ、必要な毎月積立額が算出されます。
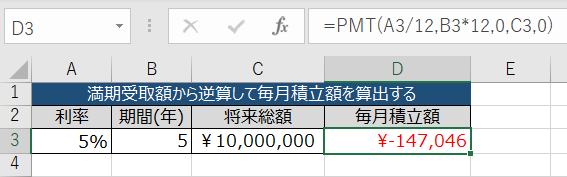
念のため、2点補足をします(読み飛ばしても差し支えありません)
- PMT関数をはじめ、財務系の関数では支払額がマイナスの値で表示されます。よって、D3セルは「14.7万円の支払が必要」とご理解ください。
- D3セルの関数において「A3/12」と「B3*12」の箇所は年間単位を月間単位に直しているだけです。求めるのは毎月積立額(つまり月間単位)ですので、年利5%は12で割って月利に、5年は12を掛けて月数に変換することで、「毎月」の積立額を算出しています。
「4%ルール」で算出した金額をC列に、ご自身が保有する投資商品の想定リターンをA列に記載し、期間(B列)を調整しながら現実的な積立額を探してみてください。
何年後にFIREが実現できるかシミュレーションすることができます。
積立可能な金額から「将来資産」を計算する
これは上記のPMT関数とは逆のやり方です。
利率・期間・毎月積立額を固定として、資産が結果いくらになるのか算出する方法です
ExcelではFV関数を用います。
FVは将来価値(Future Value)の略です
=FV(利率, 期間, 定期支払額, 現在価値, 支払期日)
こちらも以下のExcelをそのまま作っていただければ完成です。
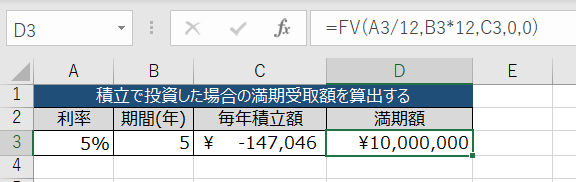
FV関数はPMT関数の逆をやっているだけです。
ご自身が保有する投資商品の想定リターンをA列に記入、投資を続ける期間をB列に記入し、毎月積立できそうな金額(C列)調整しながら、満期額(D列)をチェックしてみてください。
C列(毎月積立額)はマイナスで入力します。
こちらの算出方法の方が、毎月の生活がイメージできて良いかもしれませんね。
「毎月○万円の積立なら可能だから、△年後にサイドFIREはいけるかも」といった試算が可能です。
おわりに
今回はFIREにはいくら必要なのか、具体的な計算方法も併せてご紹介しました。
「4%ルール」も一つの目安に過ぎず、いろんなFIRE計画があってよいと思います。
目標達成までの道筋をクリアにイメージできるほど実現可能性が高くなることは間違いないので、是非Excelを駆使してライフプランを立てていってください。
では、素敵な投資ライフをお過ごしください。













